Unit 7 polar and parametric equations answers – Welcome to the realm of polar and parametric equations, a fascinating branch of mathematics that empowers us to describe and analyze curves in intricate and versatile ways. Embark on a journey through this captivating topic, where we unravel the secrets of polar coordinates and parametric representations, unlocking a world of complex and mesmerizing curves.
Polar equations provide an alternative coordinate system that elegantly describes curves using distance from a fixed point and angle measure. Parametric equations, on the other hand, offer a dynamic approach to curve definition, allowing us to express coordinates as functions of a parameter.
Together, these powerful tools provide a comprehensive framework for representing and understanding the geometry of curves.
Polar Equations: Unit 7 Polar And Parametric Equations Answers
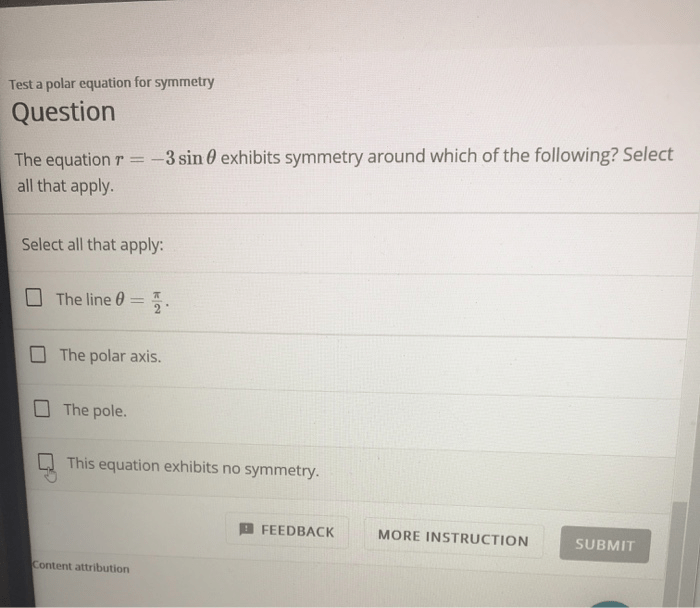
Polar coordinates are a two-dimensional coordinate system that uses the distance from a fixed point (the origin) and the angle between a fixed line (the polar axis) and the line connecting the point to the origin.
Polar equations are equations that describe curves in terms of polar coordinates. They are typically written in the form r= f( θ), where ris the distance from the origin and θis the angle between the polar axis and the line connecting the point to the origin.
Some common examples of polar equations include:
- r= 1: A circle of radius 1
- r= 2 cos( θ): A cardioid
- r= 2 sin( θ): A lemniscate
Polar coordinates can be converted to rectangular coordinates using the following formulas:
- x= rcos( θ)
- y= rsin( θ)
Parametric Equations
Parametric equations are a way of describing curves in terms of two or more parameters. They are typically written in the form x= f( t) and y= g( t), where tis a parameter that varies over a specified interval.
Some common examples of parametric equations include:
- x= t, y= t2: A parabola
- x= cos( t), y= sin( t): A circle
- x= t, y= e–t: An exponential curve
The parameter tcan be thought of as a “time” variable. As tvaries, the point ( x, y) moves along the curve.
Applications of Polar and Parametric Equations

Polar and parametric equations are used in a wide variety of applications, including:
- Physics:Describing the motion of objects in two dimensions
- Engineering:Designing curves for bridges, roads, and other structures
- Computer graphics:Creating 3D models and animations
- Biology:Modeling the growth of cells and organisms
Polar and parametric equations are powerful tools that can be used to describe a wide variety of curves. They are essential for understanding many important concepts in mathematics, science, and engineering.
Detailed FAQs
What are the key differences between polar and parametric equations?
Polar equations describe curves using distance and angle, while parametric equations define curves using functions of a parameter. Polar equations are often used for curves with radial symmetry, while parametric equations offer greater flexibility in representing complex shapes.
How are polar and parametric equations used in real-world applications?
Polar equations find applications in fields such as navigation, acoustics, and planetary motion. Parametric equations are widely used in computer graphics, animation, and robotics for modeling and animating complex objects.
What are the advantages of using polar and parametric equations?
Polar equations simplify the representation of curves with radial symmetry, while parametric equations provide a flexible framework for describing curves with intricate shapes. Both representations offer powerful tools for analyzing and understanding the geometry of curves.